A. The SI System
Measurements in the scientific world, and increasingly, in the nonscientific
world are made in SI (Système International) units. The system was established
in order to allow comparison of measurements made in one country with those
made in another. SI units and their relative values were adopted by an international
association of scientists meeting in Paris in 1960. Table 2.1 lists the basic
SI units and derived units. Notice that metric units are part of this system.
The system still in common, nonscientific use in the United States is called
the English system, even though England, like most other developed countries,
now uses metric units. Anyone using units from both the English and SI systems
needs to be aware of a few simple relationships between the two systems. These
relationships also are given in Table 2.1.
TABLE 2.1
Units of the SI system, units derived from the SI system, and their relationship
to several English units.
Property
being
measured |
Basic
SI Unit |
Derived units |
Relationship
to English Unit |
| length |
meter (m) |
kilometer (km)
1 km = 1000 m
centimeter (cm)
1 cm = 0.01 m |
1 m = 39.37 in.
1.61 km = 1 mi
2.54 cm = 1 in. |
| mass |
kilogram (kg) |
gram (g)
1 g = 0.001 kg |
1 kg = 2.204 lb
453.6 g = 1 lb |
| volume |
cubic meter (m3) |
liter (L)
1 L = 0.001 m3
cubic centimeter (cm3, cc)
1 cm3 = 0.001 L
milliliter (mL)
1 mL = 1 cm3 |
1 L = 1.057 qt
946 mL = 1.0 qt
|
| temperature |
Kelvin (K) |
Celsius (C)
K = °C + 273.15 |
| Fahrenheit (F) |
| °C = |
°F - 32 |
|
| 1.8 |
| = 5/9 (°F - 32) |
|
| energy |
joule (J) |
calorie (cal)
1 cal = 4.184 J
kilocalorie (kcal)
1 kcal = 1000 cal |
|
Two features of the SI system make it easy to use. First, it is a base-10 system;
that is, the various units of a particular dimension vary by multiples of ten.
Once a base unit is defined, units larger and smaller than the base unit are indicated
by prefixes added to the name of the base unit. Table 2.2 lists some of these
SI prefixes,along with the abbreviation for each and the numerical factor relating
it to the base unit.

| TABLE 2.2 Prefixes used in the SI system |
| Prefix |
Symbol |
Base unit multiplied by |
| mega- |
M |
1,000,000, or 106 |
| kilo- |
k |
1,000, or 103 |
| deci- |
d |
0.1, or 10-1 |
| centi- |
c |
0.01, or 10-2 |
| milli- |
m |
0.001, or 10-3 |
| micro- |
µ |
0.000001, or 10-6 |
| nano- |
n |
0.000000001, or 10-9 |
| pico- |
p |
0.000000000001, or 10-12 |
|
|
*Exponential notation is discussed in Section 2.2B.
Note here that a positive exponent means
"raised to a power." Thus 102 is 10 X 10 or "10 squared."
A negative exponent means "divided by that
power of 10," thus 10-2 is 1/100 or 0.01.
|
The tutorials illustrate the use of these prefixes. Be sure to do these problems
since only by doing problems on your own will you know whether you can solve them.
The second feature that increases the usefulness of the SI system is the direct
relationship between the base units of different dimensions. For example, the
unit of volume (cubic meter) is the cube of the unit of length (meter). We shall
see later how the unit of mass is related to the unit of volume.
The base unit of length in the SI system is the meter(m). The meter, approximately
10% longer than a yard, is equivalent to 39.37 inches, or 1.094 yards. The metric
units of length most commonly used in chemistry are listed in Table 2.3 and illustrated
in Figure 2.1. 
TABLE 2.3 Units of length in the SI system
| Unit of length |
Relationship to base unit |
| kilometer (km) |
1 km = 1000 m |
| meter (m) |
|
| decimeter (dm) |
10 dm = 1 m |
| centimeter (cm) |
100 cm = 1 m |
| millimeter (mm) |
1000 mm = 1 m |
| micrometer (µm) |
106 µm = 1 m |
| nanometer (nm) |
109 nm = 1 m |
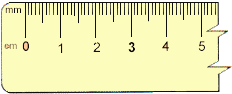
|
FIGURE 2.1 Each centimeter contains 10 millimeters.
|

The base unit of volume in the SI system is the cubic meter (m3). Other commonly used units of volume are the liter (L),
the cubic centimeter (cm3 or cc), and the milliliter (mL).
One liter has a volume equal to 0.001 m3. The nearest unit of comparable volume in the English system is the quart (1.000 L = 1.057 qt). The SI units of volume are summarized in Table 2.4 and illustrated in Figure 2.2. Note particularly that the volume of 1 cm3 is the same as the volume of 1 mL.

The standard of mass in the SI system is the kilogram (kg). A safe in Sèvres,
France, holds a metal cylinder with a mass of exactly 1 kg. The mass of that
cylinder is the same as the mass of 1000 mL (1 L) of water at 4°C, thereby
relating mass to volume. The most commonly used SI units of mass are listed
in Table 2.5. Notice that the base unit of mass in the SI system is the gram
(g), even though the standard of mass in this system is the kilogram.

TABLE 2.4 Units of volume in the SI system
| Unit of volume |
Relationship to liter |
| liter (L) |
|
| milliliter (mL) |
1000 milliliters = 1 liter |
| cubic centimeter (cm3, cc) |
1000 cubic centimeters = 1 liter |
| microliter (µL) |
106 microliters = 1 liter |

| FIGURE 2.2 The large cube measures 10 centimeters on a side and has a volume of 1000 cm3, or 1 L. The small cube next to the large one has a volume of 1 cm3, or 1 mL.
|
B. Mass and Weight
In discussing SI units we have used the term mass rather than the more familiar term weight. Mass is a measure of the amount of matter in a particular sample. The mass of a sample does not depend on its location; it is the same whether measured on Earth, on the moon, or anywhere in space. Weight is a measure of the pull of gravity on a sample and depends on where the sample is weighed.
| TABLE 2.5 Units of mass in the SI system |
| Unit of mass |
Relationship to base unit |
| kilogram (kg) |
|
| gram (g) |
1000 g = 1 kg |
| milligram (mg) |
1000 mg = 1 g |
| microgram (µg) |
106µg = 1 g |
|
Astronauts traveling in space and landing on the moon have experienced the difference between mass and weight. In Earth's gravitational field at sea level, a particular astronaut may weigh 198 pounds. On the surface of the moon, this astronaut still has the same mass, but his weight (33 pounds) is only one-sixth of what it is on Earth, because the gravitational field of the moon is much weaker than that of the Earth. In outer space the astronaut is weightless, but his mass remains unchanged.

|
FIGURE 2.3. Balances of several types. (a). Classical balance with
weighing pans suspended from a straight beam; (b). a common laboratory
balance which weighs to about 0.01 grams. The three beams give rise to the
balance's common name of triple beam balance; (c) an electronic balance
which weighs rapidly to 0.0001 g. (d) a simple top loading electronic balance.
|
Weight and mass are measured on different instruments. Mass is measured on a balance
(Figure 2.3). An object of unknown mass is put at one end of a straight beam and objects of known mass are added to the other end until their mass exactly balances that of the object whose mass is being measured. Because both ends of the beam, at the moment of balancing, are the same distance from the center of the Earth, this measurement is independent of gravity. Weight, on the other hand, is measured on a scale, which determines weight by measuring the distortion of a spring. Such a measurement depends on the pull of gravity. You will weigh less at the top of a mountain than you do in the valley below, because the pull of gravity decreases as you move further from the Earth's center. Nevertheless, your mass is the same in both places.
Despite the clear difference in meaning between the terms mass and weight, measuring the mass of an object is often called "weighing," and the terms mass and weight are frequently and incorrectly used interchangeably. Remember that the correct way to describe the amount of matter in a sample is to state its mass.
